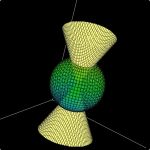
Московский физико-технический институт
Московский физико-технический институт (Физтех) – ведущий вуз России по подготовке высококвалифицированных специалистов по передовым направлениям науки и техники. Входит в топ 5 крупных рейтингов отечественных университетов. Отличительной чертой образовательного процесса МФТИ является система поиска и подготовки кадров – знаменитая «система Физтеха».